Understanding Data Mining: Extracting, Organizing, and Analyzing Large Sets of Data
| Author: | Dail Midgette |
| Level: | High School |
| Content Area: | Mathematics |
| Author: | Dail Midgette |
| Level: | High School |
| Content Area: | Mathematics |
Some basic R© commands are summarized below:
| Command | Use |
|---|---|
| set.seed( ) | To ensure that results are the same each time |
| runif() | To generate values of variables |
| plot() | To create a scatterplot of data |
| lm() | To generate a linear model |
| lines() | To add linear model to scatterplot |
| anova() | To generate an analysis of variance |
| step() | To do forward, backward, or stepwise selection |
| summary() | To summarize large results |
| title() | To give a scatterplot a title |
| cbind() | To organize imported data into rows and columns |
| write.table() | To organize data into a table |
Some additional information:
In their simplest forms, students study linear models in Algebra I. We use graphing calculators to find linear regression models of data sets, and we then use these equations to make predictions about other observations. In Algebra I, students write their equations in slope intercept form, 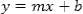 .
.
Moving beyond the Algebra I classroom, linear models tend to change in appearance. Instead of just focusing on a single independent variable and a single dependent variable, a linear model can also be used to study multiple independent variables. In this case, the general form of a linear model is:
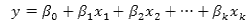
where 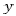 is the dependent/response variable,
is the dependent/response variable, 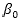 represents the coefficients of the intercepts, and
represents the coefficients of the intercepts, and 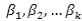 represent the regression coefficients of the predictor values
represent the regression coefficients of the predictor values 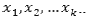 .
.
Regardless of their form or appearance, linear models are useful because they are the best equations to summarize datasets. Also, linear models are frequently used to make predictions for new observations. The linear models show general patterns in data, and as such, they allow us to engage in conversations about data that we wouldn’t be able to if we had to look at the whole set at once.
In Algebra I, students study data sets with one predictor variable and one response variable. However, in the real world, most response variables have numerous predictor variables, many of which may have a significant impact on the data. These different variables may also have differing effects on the situation at hand, so it is important to identify their effects and then use them appropriately to make sound, more valid predictions.
Sometimes, there may be very large numbers of variables involved in a set of data. Some of these variables might interfere with other variables, and some variables might be irrelevant. As a result, we must utilize variable selection techniques to improve our ability to make good predictions and to better observe the impact of specific subsets of variables.
Numerous methods of variable selection exist. At this point, our focus is on some of the traditional methods—forward, backward, and stepwise selection.
Wikipedia
http://en.wikipedia.org/wiki/Data_mining
Evolution of Data Mining
http://www.thearling.com/text/dmwhite/dmwhite.htm
The R© Project for Statistical Computing
http://www.r-project.org/
The purpose of this lesson is to provide students with an opportunity to learn about R within the confines of a topic they have worked with previously. My original intention was to use this with my Algebra I students when they study linear regression, because I think that Algebra I students, in particular, need exposure to multiple ways of accomplishing a task. Not only does R challenge them to think logically by using code, but it gives students an opportunity to see how some people really do use math in the “real world” and how much of a role math plays in life. This lesson could be used in isolation from the other two lessons in the set, but utilizing the instructional unit as a whole could give students a chance to see math in the big picture. My hope is that Algebra I students can see the mathematical realities that those people in the “real world” deal with on a daily basis, as well as to experience mathematical adventures that don’t always exist in the confines of a traditional mathematics classroom.